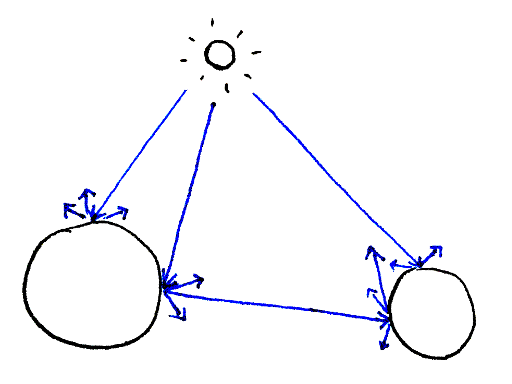
Light rays bouncing off geometry. Notice the indirect bounces.
When rendering 3D graphics, there are two questions we want to answer:
We will build up the answers to these two questions in parallel.
At a minimum, we need a world populated with objects, i.e. geometry. The world also contains light sources, which scatter light rays onto the geometry. Based on physical properties of the geometry, the light bounces off the geometry again and again, illuminating the scene. This is the basis of the rendering equation.
Light rays bouncing off geometry. Notice the indirect bounces.
To actually view this scene, we place a camera in the world. This is analogous to our eyes. Light rays bouncing off the geometry converge at the camera, and we record where those rays end up on an imaginary canvas called the image plane. In doing so, we have to determine what is actually visible to each point on the image plane.
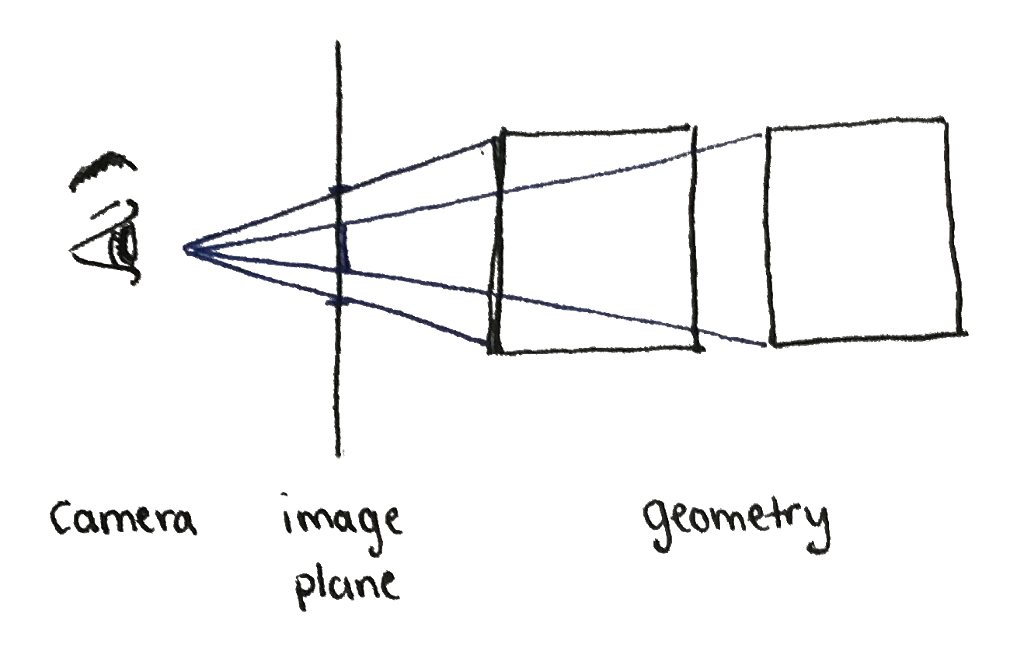
Light rays originating from the geometry converge at the camera, passing through the image plane. The convergence causes objects farther from the camera to appear smaller, an effect known as perspective.
There are two approaches to solving the visibility problem. The conceptually simple approach is ray tracing, which simulates light rays reaching the camera by sending out rays from the camera, then tracing its path as it travels to a light source. This maps well to how light physically travels in the real world, making it simple to simulate real-world effects such as shadows and reflections. These effects are collectively known as global illumination.
An example of a ray traced image, demonstrating global illumination effects such as shadows, reflection and refraction. Via Wikimedia Commons.
However, this simulation is slow. An alternate approach is rasterization. In this approach, we first project the geometry onto the image plane, then work directly on the perspective-corrected representation of the geometry. This approach can be implemented more efficiently, but at the cost of increased complexity. Global illumanation effects need to be special-cased one by one, often requiring multiple rendering passes and pre-computation ("baking").
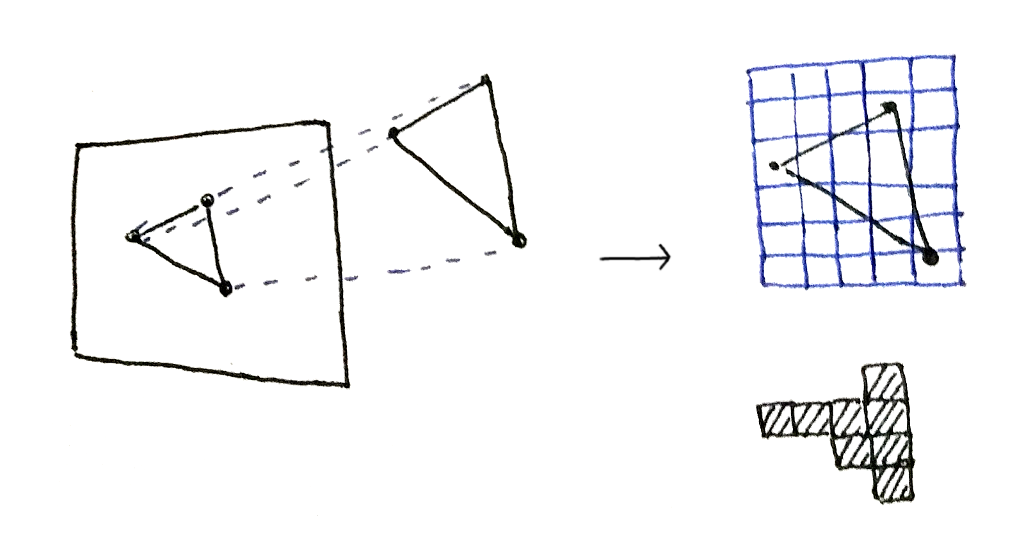
Rasterization works by projecting the geometry onto the image plane, then checking which pixels on the plane are covered by the projected geometry.
Ray tracing is usually used for offline rendering, such as in Pixar films, and rasterization for realtime graphics, such as games. The latter is the approach used by GPUs.
In this course, we will focus on ray tracing. It closely mirrors the intuition we have about how light interacts with the world, and we can avoid the more complicated math in the initial stages of development. This lets us build up our renderer in small pieces. The concepts we will use are foundational, so they carry over to real-time rendering techniques, which approximate the same light transport in different ways.