A vector `vec bbv`, with three coordinates.
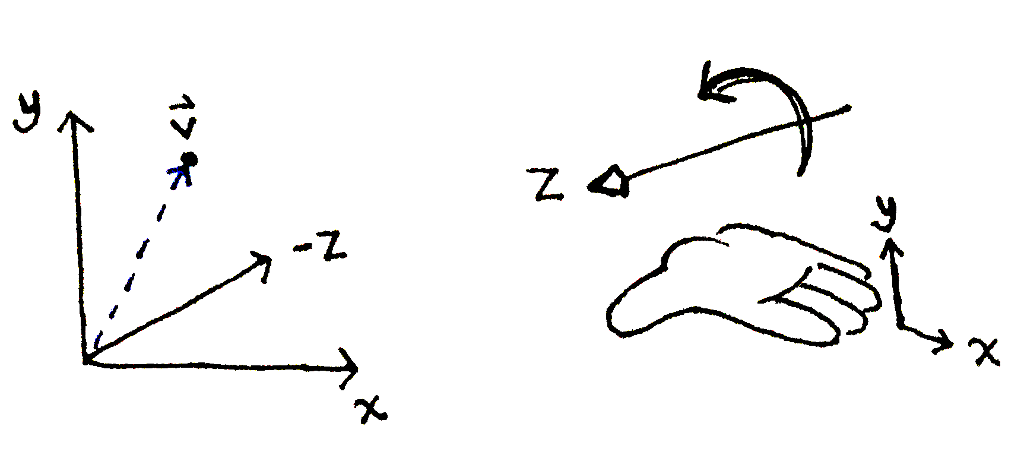
A right-handed coordinate system. Starting with your right fingers pointed toward the positive `x` axis, curl your fingers toward the positve `y` axis. Your thumb points toward the positive `z` axis.
A point in 3 dimensions can be represented as distances along 3 axes. The distances are known as the coordinates. The axes, labeled `x`, `y` and `z`, are—by convention—arranged in a right-handed coordinate system.

A vector `vec bbv`, with three coordinates.
A right-handed coordinate system. Starting with your right fingers pointed toward the positive `x` axis, curl your fingers toward the positve `y` axis. Your thumb points toward the positive `z` axis.
To differentiate between a vector and a scalar (a non-vector, numerical value), we will write the name of a vector in bold, with an arrow on top. A vector can also be written as its three components in between angle brackets.
\begin{align} \vec{\mathbf{v}} & = \langle x, y, z \rangle \\ \end{align}
The sum of two vectors is the vector obtained by following the two vectors from the origin of the coordinate system one by one. The difference of the two vectors is the vector obtained by starting at the tip of the second vector and travelling to the tip of the first. Both operations can be performed by adding or subtracting the individual coordinates of the two vectors.
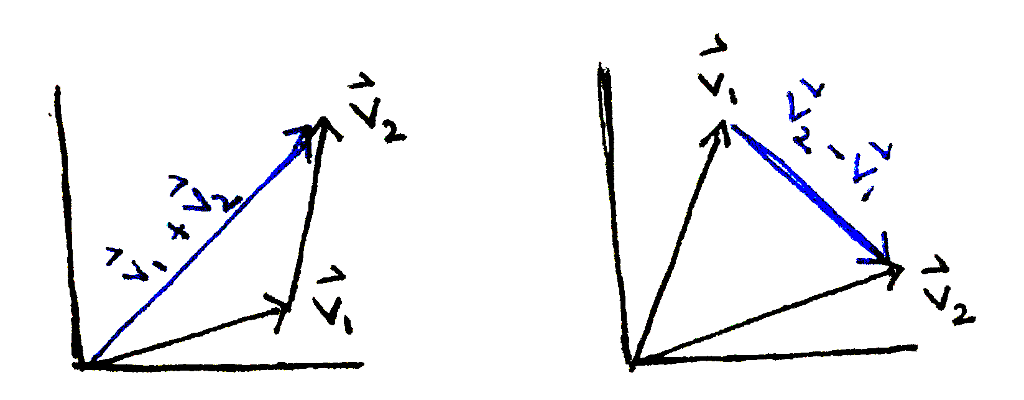
The sum and difference of two vectors `vec bbv_1` and `vec bbv_2`.
\begin{align} \vec{\mathbf{v}_1} & = \langle a, b, c \rangle \\ \vec{\mathbf{v}_2} & = \langle d, e, f \rangle \\ \vec{\mathbf{v}_1} + \vec{\mathbf{v}_2} & = \langle a + d, b + e, c + f \rangle \\ \vec{\mathbf{v}_2} - \vec{\mathbf{v}_1} & = \langle d - a, e - b, f - c \rangle \\ \end{align}
A vector can be scaled by a scalar, stretching or squashing the vector. The operation is performed by scaling each coordinate of the vector by the scalar.
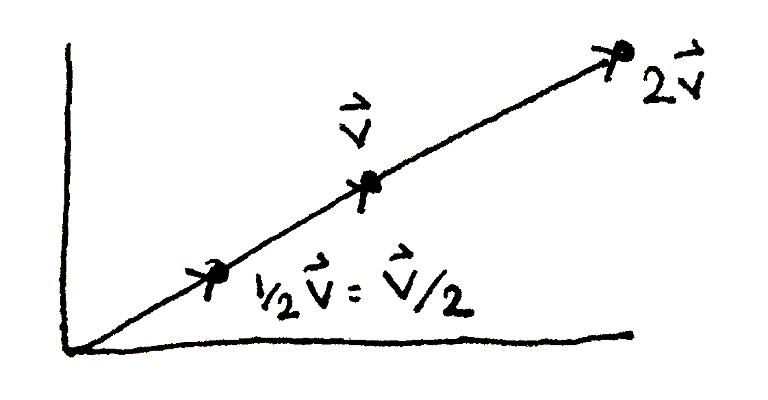
A vector `vec bbv` scaled by `1/2` and by `2`.
\begin{align} \vec{\mathbf{v}} & = \langle a, b, c \rangle \\ k \vec{\mathbf{v}} & = \langle ka, kb, kc \rangle \end{align}
With these pieces, we can now represent a ray originating at `vec bbo` and passing through `vec bbp` as two vectors: