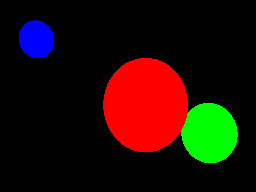
Project 2: Rendering unshaded spheres

Goals

• Represent geometry in the scene
• Perform intersection tests to determine visibility

In this project, we will add a set of spheres to the world, then rendered them with no lighting. Each sphere can be given its own color, giving us an image like this one:

Three unshaded spheres.

Add spheres to the world

Create a representation of a sphere consisting of two pieces of information:

• A center point. This is the location of the sphere, as a 3D vector.
• A radius. This is just a scalar.

Add a few of these spheres into the scene.

Add color to the spheres

As you've seen in the previous project, a color consists of red, green and blue components, each in the range of `[0, 255]`. Because we're going to combine multiple colors in future lessons, we will represent colors with components in the range `[0, 1]`. Then, we will convert this into a range our pixel plotting function can accept at the very end, right before plotting a pixel.

Represent a color with three non-integer components, each between zero and one. Add one more piece of information to the representation of each sphere: its color.

Perform ray-sphere intersection tests

For each of the rays you created in the previous project, loop through all the spheres in the scene and perform an intersection test on them. Recall that we found a quadratic equation encoding the solutions of the intersection test:

\begin{array} \\a & t^2 & + & b & t & + & c & = & 0 \\ \left( \Vert \vec{\mathbf{d}} \Vert ^ 2 \right) & t^2 & + & \left( 2 \langle \vec{\mathbf{c}'}, \vec{\mathbf{d}} \rangle \right) & t & + & \left( \Vert \vec{\mathbf{c}'} \Vert ^ 2 - r^2 \right) & = & 0 \end{array}

The variables here are:

• `vec bbd` is the direction vector for the ray.
• `vec bbc'` = `vec bbo - vec bbc`, where `vec bbo` is the origin of the ray, and `vec bbc` is the center of the sphere.
• `r` is the radius of the sphere.
• `t` is the value we're solving for. Out of all possible solutions, we want the lowest one.

Using the quadratic formula, we know the solutions to this equation are:

• `t = {-b +- sqrt{b^2 - 4 a c}} / {2a}`

Start by calculating `a`, `b` and `c`. You'll need to support taking the dot product of two vectors.

Next, calculate the discriminant, that is the quantity `b^2 - 4ac`. There are two possibilities:

• The discriminant is negative. In that case, `t` cannot be a real number, so the ray does not intersect with the sphere.

• The discriminant is zero or positive. We can treat these two cases the same. Calculate the two values of `t` using the quadratic formula and pick the smaller one.

  Only pick values of `t` that are positive. Remember that a negative value means the intersection happens before the image plane, maybe even behind the camera. If neither value of `t` is positive, the ray does not intersect the sphere.

Figure out which sphere a ray sees

After performing all the intersection tests for a single ray, there are two possibilties:

• The ray does not intersect any sphere. Color the corresponding pixel black.

• The ray intersects at least one sphere. Out of the spheres the ray intersects, pick the one with the lowest `t`. Color the corresponding pixel the color of that sphere.

In the reference image, we added three spheres of three different colors. The resulting image looks like this: