A collection of vectors with the same length.
You don't need to understand all the math in this section. What's important is knowing the terms (highlighted in yellow), and bolded sections at the bottom.
Every vector has a length, also known as a norm or magnitude. The length of a vector `vec bbv` is denoted `||vec bbv||`. A vector with length `1` is called a unit vector, often denoted `hat bbv`.

A collection of vectors with the same length.
Given a vector with coordinates `x`, `y` and `z`, the Pythagorean theorem tells us the vector's length is `sqrt{x^2 + y^2 + z^2}`.
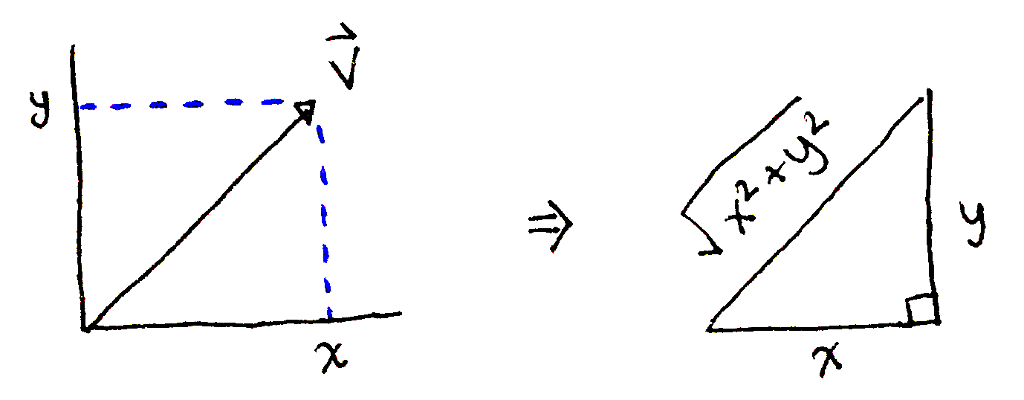
Computing the length of `vec bbv` using the Pythagorean theorem.
If we have a vector `vec bbv` that is not a unit vector, we can find a unit vector pointing in the same direction. To do this, we divide the vector by its length: `hat bbv = vec bbv / ||vec bbv||`.

A vector `vec bbv` and the unit vector pointing in the same direction, `hat bbv`.
Given two vectors `vec bba` and `vec bb b`, we can compute the projection of `vec bb b` onto `vec bba`. This is basically `vec bb b`'s "shadow" on top of `vec bba`. The projection tells us "how much" of `vec bb b` extends in the direction of `vec bba`.
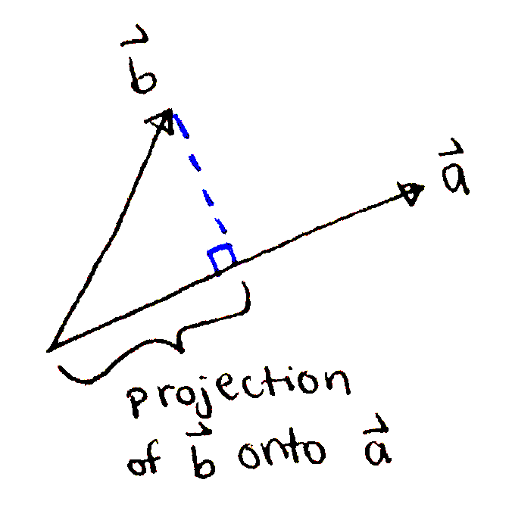
The projection of a vector `vec bb b` onto another vector `vec bba`.
With trigonometry, we can deduce the projection is `||vec bb b||cos theta`, where `theta` is the angle between `vec bba` and `vec bb b`.
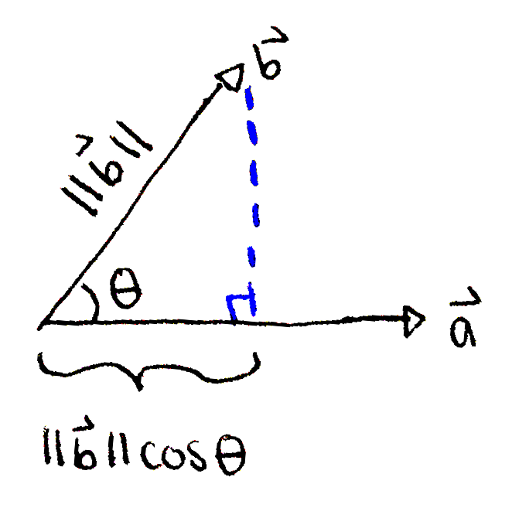
With trigonometry, we see that the projection of `vec bb b` onto `vec bba` is `||vec bb b||cos theta`.
Both geometrically and algebraically, we can verify the projection is just `||vec bb b||` when `vec bba` and `vec bb b` point in the same direction (`theta = 0^@` ⇒ `cos theta = 1`). The projection is zero when the two vectors are perpendicular (`theta = 90^@` ⇒ `cos theta = 0`). Finally, when `vec bba` and `vec bb b` point in "opposing" directions (`90^@ < theta < 270^@`), the projection is negative.
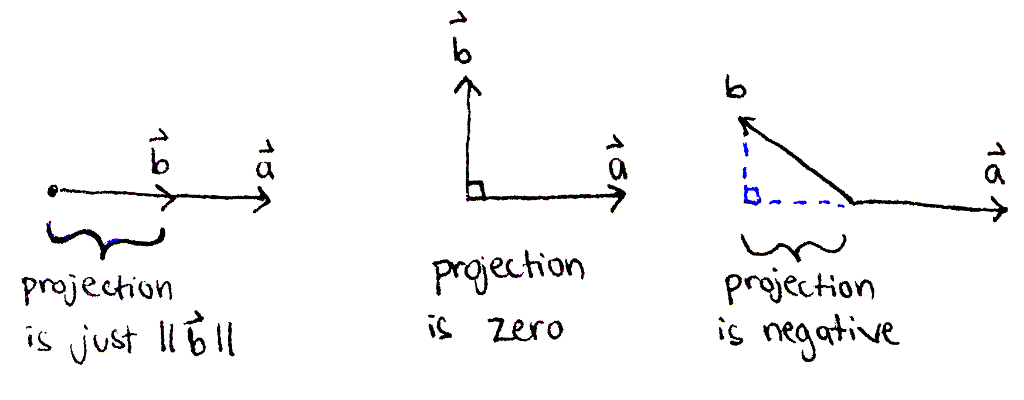
When two vectors `vec bba` and `vec bb b` point in the same direction, the projection of `vec bb b` onto `vec bba` is just the length of `vec bb b`. If the two vectors are perpendicular, the projection is zero. And if they point in opposing directions, the projection is negative.
From the projection, we can compute `||vec bba||||vec bb b||cos theta`, a quantity known as the dot product of `vec bba` and `vec bb b`. This quantity is denoted `vec bba * vec bb b` or `(:vec bba, vec bb b:)`. The important feature of the dot product is that it encodes the angle between two vectors.
With some algebra, we can compute `(:a, b, c:) * (:d, e, f:) = ad + be + cf`, that is we can compute the dot product of two vectors by multiply their corresponding coordinates and adding together the results.
This also implies that `||(:x, y, z:)||^2 = x^2 + y^2 + z^2 = (:x, y, z:) * (:x, y, z:)`, that is the squared length of a vector is the dot product of the vector with itself.
Some properties of the dot product useful in the sphere-ray intersection test: