Barebones 3D rendering with WebGL

After my recent post on getting started with WebGL, it’s time to move onto 3D rendering. It turns out, I had most of the OpenGL concepts in place already. But, what I needed to understand was what format OpenGL needed my data in order to get the results I wanted.

In this post, I’ll implement the bare minimum changes needed to implement useful 3D rendering. This entails:

I want to be clear about the audience for this post. This post is aimed towards people like myself, who understand 3D rendering concepts (homogeneous coordinates, matrix transformations, etc.) but need to connect those concepts to the OpenGL/WebGL APIs.

Culling and depth tests

Even though OpenGL leaves it up to developers to implement how rendering is done, some parts of the rendering are set in stone. Application code can specify what vertices to render, and how pixels look on screen, but OpenGL automatically decides which pixels to even paint based on some fixed code known as rasterization.

Because we’ll actually be creating a more complicated model, we want two useful features enabled:

These two features can be enabled at any time, but since we always want them for our renderer, we can enable them right as soon as we get the GL rendering context:

 const gl = canvas.getContext('webgl');

+gl.enable(gl.DEPTH_TEST);
+gl.enable(gl.CULL_FACE);

With the depth test enabled, we also need to clear the depth buffer before rendering. Otherwise, older values in the depth buffer might carry over to the new render. Do this right before the glDrawArrays call.

+gl.clear(gl.COLOR_BUFFER_BIT | gl.DEPTH_BUFFER_BIT);
 gl.drawArrays(gl.TRIANGLES, 0, 3 * 2 * 6);

Defining a mesh

The vertex shader actually generates 3D points (really 4D in homogeneous coordinates) to rasterize. That means your input to the vertex shader can be anything that you can convert into a 3D point, as long as you have one set of inputs for every point you’ll generate.

Updating the shader to handle per-vertex colors

For a basic mesh, we’ll want a 3D position (actually 3D, not 4D, because the w-coordinate will always be 1) and a color. The latter is just nice to give the various triangles their own colors, and it nicely demonstrates how we can feed two separate pieces of information into the shader. Let’s update our vertex shader to include the input color, then pass along that input color to the fragment shader:

 attribute vec3 position;
+attribute vec3 inputColor;
 varying vec4 color;

 void main() {
   gl_Position = vec4(position, 1);
-  color = gl_Position * 0.5 + 0.5;
+  color = vec4(inputColor, 1);
 }

Defining the mesh data

As we’ll see soon, we’ll keep both the base position and the color constant throughout the program, so the second option makes sense. So now, we can specify both pieces of data in a single Float32Array.

const vertexData = new Float32Array([
  // Six faces for a cube.
  // Each face is made of two triangles, with three points in each triangle.
  // Each pair of triangles has the same color.

  // FRONT
  /* pos = */ -1, -1,  1, /* color = */ 1, 0, 0,
  /* pos = */  1, -1,  1, /* color = */ 1, 0, 0,
  /* pos = */  1,  1,  1, /* color = */ 1, 0, 0,

  /* pos = */ -1, -1,  1, /* color = */ 1, 0, 0,
  /* pos = */  1,  1,  1, /* color = */ 1, 0, 0,
  /* pos = */ -1,  1,  1, /* color = */ 1, 0, 0,

  // And so on for the other five faces...
  // See the source code for this post to see the full mesh
  // ...
]);

The question is: where should we place the points? After all, where is the camera? The trick is OpenGL wants the points in a specific coordinate system, which I’ll talk about below. But, our vertex shader is the one generating points. That means we can place the input points where they’re useful for modeling purposes (e.g. around the origin like I’ve done), and the vertex shader can move them to a location the OpenGL rasterizer will actually recognize.

As an aside, you need to be careful about which order you specify the points for each triangle. Because we turned on back-face culling, you want to specify the points in counter-clockwise order when viewed from the front.

Connecting the data to the shader inputs

Finally, we can now connect both pieces of data, which are interleaved in a single byte sequence, to their corresponding shader inputs:

const vertexBuffer = gl.createBuffer();
gl.bindBuffer(gl.ARRAY_BUFFER, vertexBuffer);
gl.bufferData(gl.ARRAY_BUFFER, vertexData, gl.STATIC_DRAW);

const positionAttribute = gl.getAttribLocation(program, 'position');
gl.enableVertexAttribArray(positionAttribute);
gl.vertexAttribPointer(positionAttribute, 3, gl.FLOAT, false, 24, 0);

const colorAttribute = gl.getAttribLocation(program, 'inputColor');
gl.enableVertexAttribArray(colorAttribute);
gl.vertexAttribPointer(colorAttribute, 3, gl.FLOAT, false, 24, 12);

We’ll also need to tell the glDrawArrays call to actually render the correct number of triangles:

-gl.drawArrays(gl.TRIANGLES, 0, 3);
+gl.drawArrays(gl.TRIANGLES, 0, 3 * 2 * 6);

At this point, your program will show nothing, because the way we convert the 3D input point into a 4D gl_Position means we’re essentially inside the cube looking out. Back-face culling means the inner sides of the cube faces aren’t visible. If you turn off the culling, you’ll see a single blue square.

(Note: I’m deliberately not introducing another concept, known as an Element Buffer Object or EBO. While this concept is useful for sharing points across multiple vertices, I want to introduce only the necessary concepts right now.)

Setting up for animation

Before fixing the shader to place points in a visible location, I want to take a detour and start re-rendering the model every frame. The reason is, to view every part of the cube, we want to rotate it over time. That means we can no longer render it in a fixed orientation and leave it that way.

This part is pretty easy: just wrap the glClear and glDrawArrays calls (the two parts that are actually doing the drawing) inside a function that is called by requestAnimationFrame.

requestAnimationFrame(t => loop(gl, t));

function loop(gl, t) {
  gl.clear(gl.COLOR_BUFFER_BIT | gl.DEPTH_BUFFER_BIT);
  gl.drawArrays(gl.TRIANGLES, 0, 3 * 2 * 6);

  requestAnimationFrame(t => loop(gl, t));
}

Note the t parameter will be useful for automatically rotating the cube in the future.

There’s nothing WebGL or OpenGL-specific about this change. It’s common to do this in web animation code.

Transformations

The last step is to take the input positions, specified in a way that’s convenient for modeling, and output positions OpenGL can actually rasterize correctly. That means generating final positions that are in clip space, which is basically a 3D cube ranging from -1 to 1 in each direction. Any point inside this cube will be rasterized.

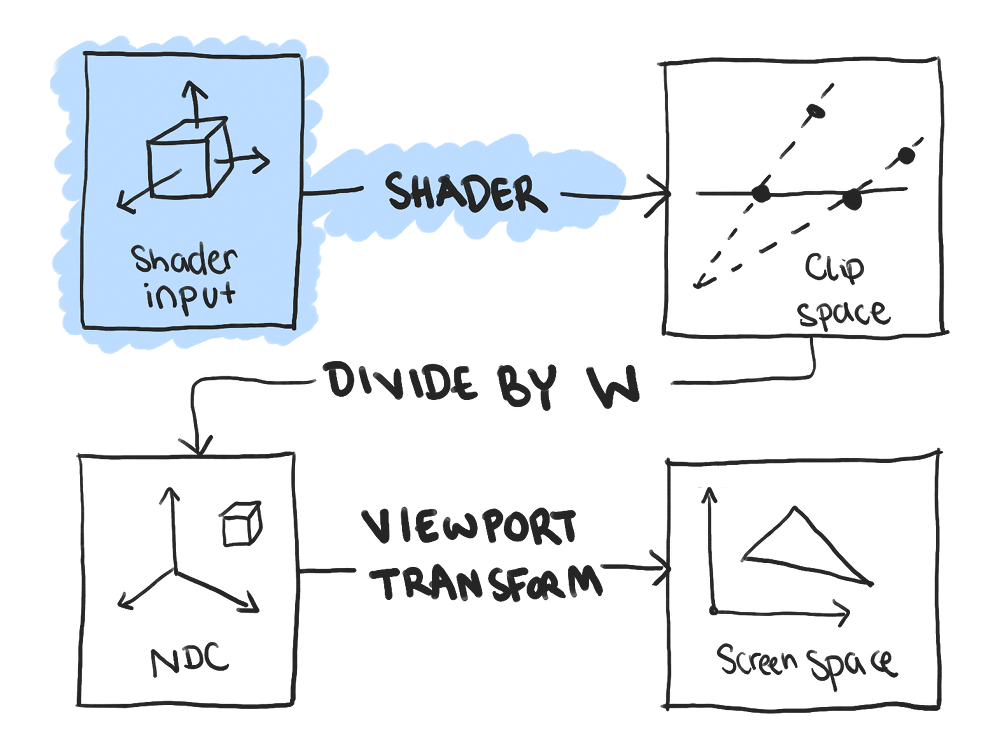
The reason for my breakdown is many tutorials talk about model, world, and view space alongside clip space, NDC and screen space. But it’s important to realize that everything before clip space is up to you. You decide what the input data looks like and how it gets converted into clip space. That probably means specifying the inputs in model space, then sequentially applying the local and camera transformations. But if you want to understand the OpenGL APIs, it’s important to first understand what’s under your control and what the OpenGL provides for you.

Here’s the cool part: if you wanted, you could pre-compute the coordinates directly in clip space and your vertex shader would just pass along the input positions to OpenGL. This is exactly what our first demo did! But, doing so per-frame is expensive, since the transformations we usually want to do (matrix multiplications) are much faster on the GPU.

Updating the shader to take in transformations

To convert from the model space coordinates specified in the VBO to clip space, let’s break up apart the transformation into two parts:

This breakdown works for our purposes, because we’ll rotate the cube over time will leaving the perspective projection the same. In real-world applications, you’d slot in a camera (or view) transformation in between the two steps to allow for a moving camera without having to modify the entire world.

Start by adding two uniform variables to the shader. Remember that a uniform is a piece of input data that is specified for an entire draw call and stays constant over all the vertices in that draw call. In our case, at any given moment, the transformations are the same for all the vertices of the triangles that make up our cube.

The two variables represent the two transformations, and therefore are 4×4 matrices. We can use the transformations by converting the input position into homogeneous coordinates, then pre-multiplying by the transformation matrices.

 attribute vec3 position;
 attribute vec3 inputColor;
+uniform mat4 transformation;
+uniform mat4 projection;
 varying vec4 color;
 
 void main() {
-  gl_Position = vec4(position, 1);
+  gl_Position = projection * transformation * vec4(position, 1);
   color = vec4(inputColor, 1);
 }

Specifying a perspective projection matrix

Let’s populate one of the two matrices above, namely the projection matrix. Remember that, because of the way our vertex shader is set up, the projection matrix will take points in world space (where the input points end up after the model transformation) and put them into clip space. That means the projection matrix has two responsibilities:

I won’t go into the math of the perspective projection matrix, as it’s covered in other places. What’s important is we’ll define the matrix in terms of some parameters, like the distance to the near and far clipping panes, and the viewing angle. Let’s look at some code:

const f = 100;
const n = 0.1;
const t = n * Math.tan(Math.PI / 8);
const b = -t;
const r = t * gl.canvas.clientWidth / gl.canvas.clientHeight;
const l = -r;

const projection = new Float32Array([
    2 * n / (r - l),                 0,                    0,  0,
                  0,   2 * n / (t - b),                    0,  0,
  (r + l) / (r - l), (t + b) / (t - b),   -(f + n) / (f - n), -1,
                  0,                 0, -2 * f * n / (f - n),  0,
]);

Now, that we have a matrix, in the correct format, we can associate it with the variable in the shader. This works somewhat similarly to how an array is associated with an attribute variable. However, because a uniform contains essentially one piece of data to be shared by all vertices (as opposed to one piece of data per vertex), there’s no intermediate buffer. Just grab a handle to the variable and send it the data.

const uniformP = gl.getUniformLocation(program, 'projection');
gl.uniformMatrix4fv(uniformP, false, projection);

Make sure to do this outside the loop function. We won’t change the projection throughout the program execution, so we only need to send this matrix once!

Specifying the model transformation matrix

A traditional projection matrix assumes points in “view space”, that is in the view of a camera. To keep things simpler, we’ll assume the camera is at the origin and looking at the negative z direction (which is what view space essentially is). So now, the goal is to transform the shader input positions into points that are within the viewable area defined by the perspective projection’s field of view and clipping planes.

The choice was pretty arbitrary, but this resulted in a cube that had most sides visible (the very back face never came into view), filled up most of the canvas, and was relative easily to calculate by hand.

I took the usual transformation matrices for these transformations (you can find them online), multiplied them in reverse order, and finally transposed them to get them into column-major order. I defined the matrices with some variables so I could easily vary the angle of rotation:

const uniformT = gl.getUniformLocation(program, 'transformation');

function loop(gl, t) {
  const a = t * Math.PI / 4000;
  const c = Math.cos(a);
  const s = Math.sin(a);
  const x = 2;
  const tz = -9;

  const transformation = new Float32Array([
     c * x,  s * s * x, -c * s * x, 0,
         0,      c * x,      s * x, 0,
     s * x, -c * s * x,  c * c * x, 0,
         0,          0,         tz, 1,
  ]);

  gl.uniformMatrix4fv(uniformT, false, transformation);

  gl.clear(gl.COLOR_BUFFER_BIT | gl.DEPTH_BUFFER_BIT);
  gl.drawArrays(gl.TRIANGLES, 0, 3 * 2 * 6);
}

Notice that the model transformation matrix is defined inside the loop function, allowing the use of the time parameter to define the angle of rotation. Otherwise, associating the resulting matrix with the shader variable is exactly the same as before.

Demo

And with all that, we have our rotating cube! (I put it behind a play button to prevent the animation from using up your battery while you read the article.)

The entire code is embedded within this post. You’ll find a large portion of the code is defining the vertex shader input data.

What’s next?

Now that I have a basic 3D rendering pipeline set up in OpenGL, I can start building on top of it. Here are some areas I’ll visit next.

Indexed drawing

I plan to do a follow up with indexed drawing, in which we can reference the same vertex multiple times in the same mesh. That saves space and computation when defining the mesh, and promotes consistency within the model.

Where’s the shading?

In legacy OpenGL, you were forced to use the shading models OpenGL provided. In modern OpenGL, you decide how to shade your models in the fragment shader code. I won’t go into the topic in this post, but basically, you output normal vectors from your vertex shader, which get interpolated across fragments and passed into the fragment shader. Then, in the fragment shader, you use the passed in normal to implement a shading model such as Phong shading.

Now can I use libraries?

Admittedly, generating the various transformation matrices is pretty painful to do by hand. However, it was important for me to understand how the theory (which I already understand) maps to the data format OpenGL expects. Now that I understand the connection, I’ll certainly use glMatrix going forward.

The manual approach is especially important for the mesh definition, where I could have used an object loader library. I’m personally interested in procedurally generating a mesh, so it’s important I understand what kind of data I need to generate.