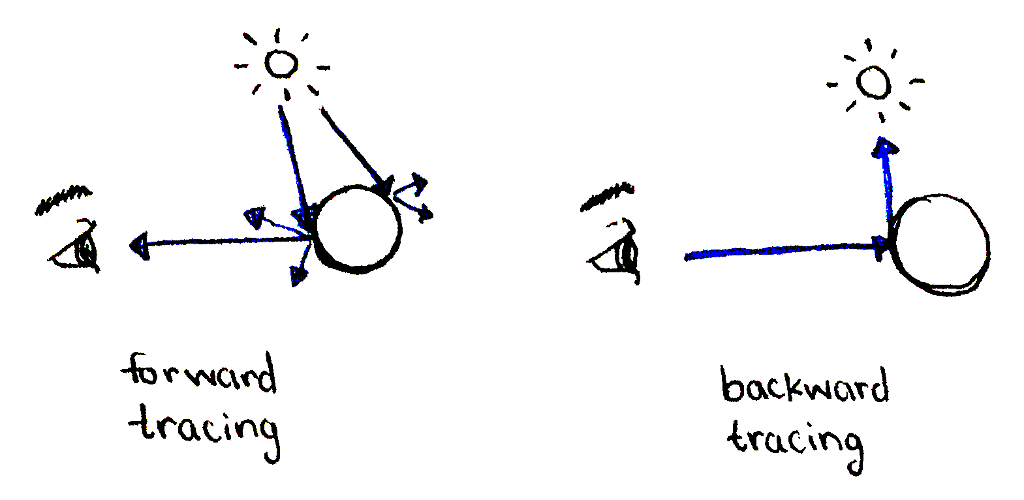
In forward tracing, most rays don't end up at the camera. In backward tracing, we only consider rays that end at the camera by starting at the camera.
This section deals with vectors. If you're not familiar with vectors, or need to brush up, please read the refresher on vectors before reading this section.
In the real world, light rays originate at light sources, run into objects, causing bounced rays to scatter in many directions. Some of the bounced rays enter our eyes—the camera—and these are the rays we see. If we were to simulate this faithfully, we would simulate many rays that we'd never see, which is a waste of computational power. Instead, in ray tracing, we go backwards: cast rays from the camera out into the world and see how they end up at the light sources.

In forward tracing, most rays don't end up at the camera. In backward tracing, we only consider rays that end at the camera by starting at the camera.
Even with backward tracing, how many rays do we cast, and which ones? To answer this, we divide the image plane into small regions, one corresponding to each pixel in the output image. Then, we construct a ray starting at the camera and passing through the center of each region.
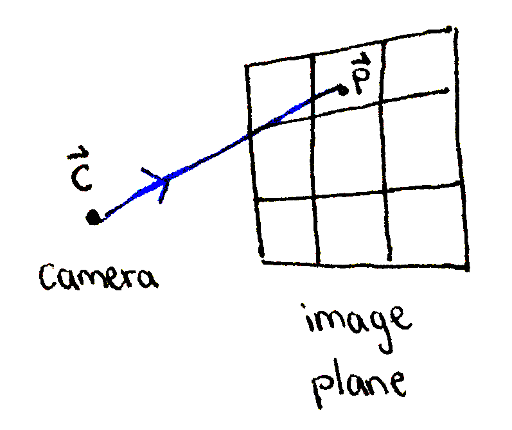
A ray is constructed, originating at the camera and passing through a point on the image plane.
The position of the camera is constant; we call it `vec bbc`. The image plane is represented by the positions of its four corners, call them `vec bbx_1`, `vec bbx_2`, `vec bbx_3` and `vec bbx_4`. Suppose we have a point `vec bbp` on the image plane. This point is some percentage `alpha in [0, 1]` (between `0` and `1` inclusive) of the distance horizontally between the left and right edges of the image plane. Similarly, it's some percentage `beta in [0, 1]` of the distance vertically between the top and bottom edges of the image plane.
To find `vec bbp`, we linearly interpolate (or lerp for short) a distance of `alpha` between `vec bbx_1` and `vec bbx_2`. This gives us a point `alpha` percent along the way on the line segment between the two vectors. We do this again between `vec bbx_3` and `vec bbx_4`, giving us a point `alpha` percent along the way on the line segment between these two vectors. Then, we take the two resulting points and lerp a distance of `beta` between them. This is known as bilinear interpolation.
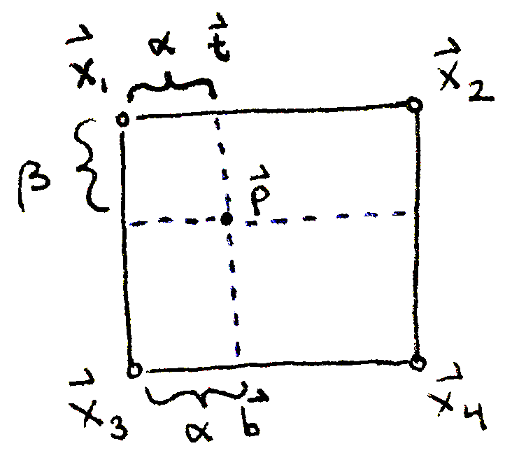
\begin{align} \vec{\mathbf{t}} & = (1 - \alpha) \vec{\mathbf{x}_1} + \alpha \vec{\mathbf{x}_2} \\ \vec{\mathbf{b}} & = (1 - \alpha) \vec{\mathbf{x}_3} + \alpha \vec{\mathbf{x}_4} \\ \vec{\mathbf{p}} & = (1 - \beta) \vec{\mathbf{t}} + \beta \vec{\mathbf{b}} \end{align}
Finally, the resulting ray is the one originating at `vec bbp`, with a direction of `vec bbo = (vec bbp - vec bbc)`. The ray could have also originated at the camera, `vec bbc`, but we don't care about the points on the ray in between the camera and the image plane. So, we'll start the ray at the image plane.